De standaardfout SE van log10(N) wordt gebruikt om de levensduur of de vermoeiingsschade te voorspellen voor een gegeven overlevingskans. Vermoeiingstest data bevatten altijd een hoeveelheid spreiding en bij een gegeven spanningsniveau wordt aangenomen dat de statistische verdeling van de vermoeiingslevensduur een log-normale verdeling is. Of in andere woorden, een normale of Gauss verdeling van het logaritme van de vermoeiingslevensduur.
De standaardfout
In de praktijk, wanneer we een voorspelling van de levensduur of de schade willen maken, gebruiken we een opzoektabel (zie Tabel 1 hieronder) om de afwijking van de gemiddelde (50%) levensduur in termen van de standaardfout te bepalen.
De waardes in de tabel worden berekend aan de hand van de kansdichtheidsfunctie (PDF) en de cumulatieve kansverdelingsfunctie (CDF) van de normale verdeling.
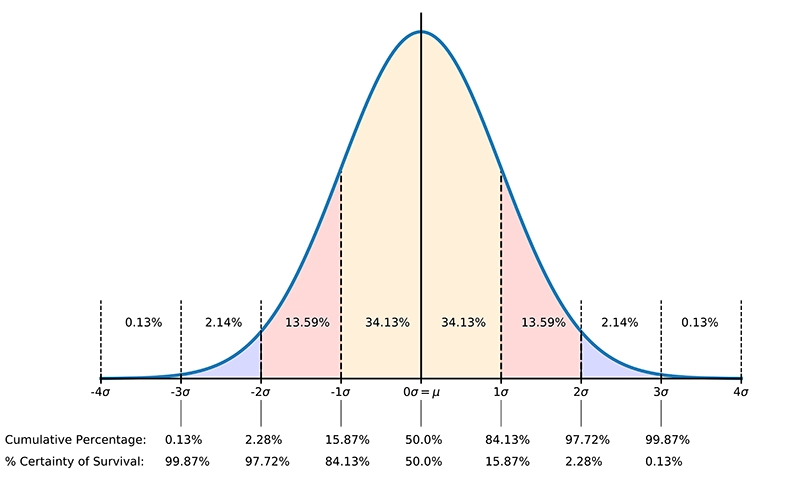
De kansdichtheidsfunctie (PDF) is de curve van de normale verdeling, zoals weergegeven in Afbeelding 1 hieronder:
$${\displaystyle {\frac {1}{\sigma {\sqrt {2\pi }}}}\;\exp \left(-{\frac {\left(x-\mu \right)^{2}}{2\sigma ^{2}}}\right)}$$
Waarbij:
- $\mu$ het gemiddelde van de data
- $\sigma$ de standaard afwijking van het gemiddelde
De cumulatieve kansverdelingsfunctie is de integraal van de PDF:
$${\displaystyle {\frac {1}{2}}\left(1+\mathrm {erf} \,{\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)}$$
Het percentage overlevingskans is dan $1 - CDF$ (zie ook Afbeelding 1).
| Aantal standaard afwijkingen van het gemiddelde | % Overlevingskans |
|---|---|
| -5 | 99.99997 |
| -4 | 99.997 |
| -3 | 99.87 |
| -2 | 97.72 |
| -1 | 84.13 |
| 0 | 50 |
| 1 | 15.87 |
| 2 | 2.28 |
| 3 | 0.13 |
| 4 | 0.003 |
| 5 | 0.00003 |
Berekeningsvoorbeeld
Laten we als voorbeeld een component beschouwen dat een cyclische spanning ondergaat met een constante amplitude, variërend tussen +300 en -300 MPa. Het onderdeel is gemaakt uit een materiaal waarvan we de parameters van de S-N curve kennen voor een overlevingskans van 50%. Deze parameters zijn:
- snijpunt met as spanningsinterval $SRI$ = 1300 MPa
- de helling van de curve ${b}_{1}$ = -0.0612
- standaardfout $SE$ = 0.12
De bovenstaande parameters definiëren een S-N curve in termen van het spanningsinterval en niet de spanningsamplitude. Het spanningsinterval Sr is een functie van het aantal belastingscycli N:
$${\displaystyle S_r = SRI \cdot N^{b_1}}$$
In ons geval is het spanningsinterval 2 ⋅ 300 MPa = 600 MPa. Het voorspelde aantal cycli tot bezwijken van het component, op basis van een overlevingskans van 50% is:
$${\displaystyle 600 = 1300 \cdot N_{50}^{-0.0612}}$$
of ${\displaystyle N_{50}}$ = 306760 cycles.
We willen nu een design S-N curve gebruiken (typisch wordt een design S-N curve gebaseerd op een overlevingskans van 97.7%) en niet de gemiddelde S-N curve. Wat is nu het voorspelde aantal cycli tot bezwijken van het component op basis van een overlevingskans van 97.7%?
Vooreerst moet we het aantal standaard afwijkingen t.o.v. het gemiddelde kennen dat overeenkomt met een overlevingskans van 97.7%. In tabel 1 vinden we n = -2 voor een overlevingskans van 97.7%.
De S-N curve wordt aangepast door de curve naar links te verschuiven, of anders gezegd, het aantal cycli te reduceren bij eenzelfde spanningsinterval:
$${\displaystyle log_{10}(N) = log_{10}(N_{50}) - n \cdot SE}$$
of anders uitgedrukt:
$${\displaystyle N = N_{50} \cdot 10^{(-n \text{ } \cdot \text{ } SE)}}$$
$${\displaystyle N_{97} = 306760 \cdot 10^{(-2 \text{ } \cdot \text{ } 0.12)}}$$
Dit geeft ons ${\displaystyle S_{97}}$ = 176522 cycli, of een reductie van 42% in levensduur t.o.v. N50.